python 已知平行四邊形三個點,求第四個點的案例
我就廢話不多說了,大家還是直接看代碼吧!
import numpy as np#已知平行四邊形三個點,求第四個點#計算兩點之間的距離def CalcEuclideanDistance(point1,point2): vec1 = np.array(point1) vec2 = np.array(point2) distance = np.linalg.norm(vec1 - vec2) return distance#計算第四個點def CalcFourthPoint(point1,point2,point3): #pint3為A點 D = (point1[0]+point2[0]-point3[0],point1[1]+point2[1]-point3[1]) return D#三點構成一個三角形,利用兩點之間的距離,判斷鄰邊AB和AC,利用向量法以及平行四邊形法則,可以求得第四個點Ddef JudgeBeveling(point1,point2,point3): dist1 = CalcEuclideanDistance(point1,point2) dist2 = CalcEuclideanDistance(point1,point3) dist3 = CalcEuclideanDistance(point2,point3) dist = [dist1, dist2, dist3] max_dist = dist.index(max(dist)) if max_dist == 0: D = CalcFourthPoint(point1,point2,point3) elif max_dist == 1: D = CalcFourthPoint(point1,point3,point2) else: D = CalcFourthPoint(point2,point3,point1) return D print(JudgeBeveling((0,1),(1,0),(1,1)))print(JudgeBeveling((5,39),(500,35),(496,17)))
補充知識:計算圖像中任意四個點連成的四邊形面積與Ground truth的IOU(Python)
1.先求任意四個點連成四邊形的面積
這個問題可以用下面的圖簡單的看一下
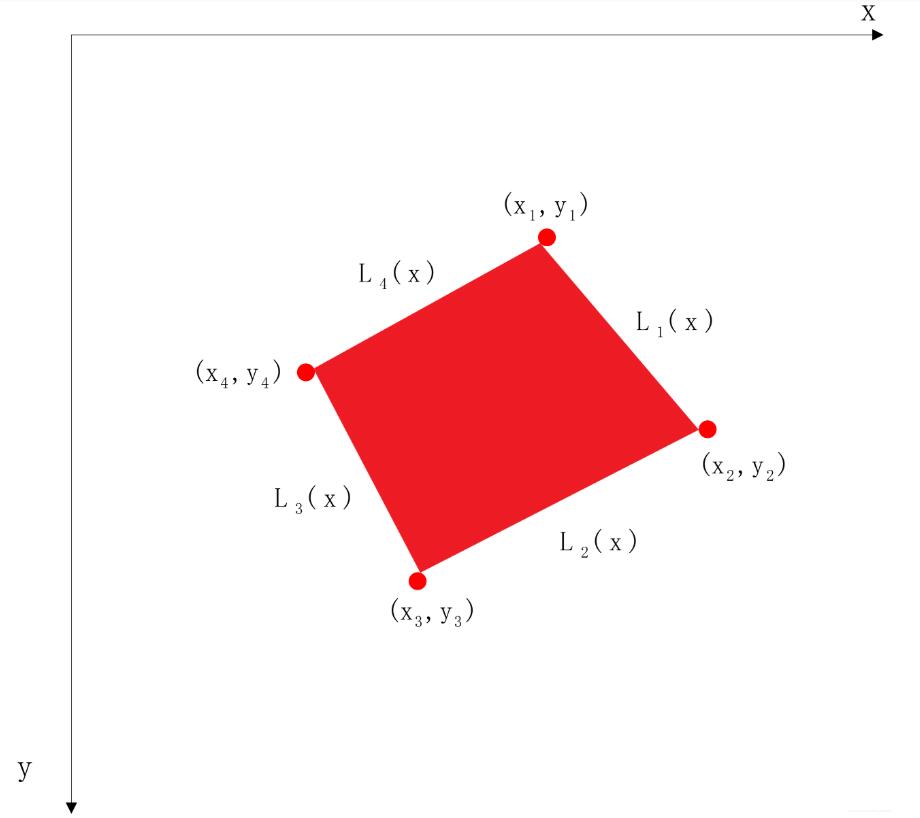
圖像的坐標如上圖所示,大致的想法就是四個點可以確定四條線,然后進行判斷,在紅色區域中則為面積中的一個像素,否則不在。先求四條線的斜率
def line_slope(x1,y1,x2,y2,x3,y3,x4,y4): k1=(y2-y1)/(x2-x1) k2=(y3-y2)/(x3-x2) k3=(y4-y3)/(x4-x3) k4=(y1-y4)/(x1-x4) return k1,k2,k3,k4
然后計算每個位置上的各個函數值
l1=int(tk1*(i-tx1)+ty1)l2=int(tk2*(i-tx2)+ty2)l3=int(tk3*(i-tx3)+ty3)l4=int(tk4*(i-tx4)+ty4)
判斷條件很重要,因為左邊是那樣排列的,所以判斷條件就是
(l1<=j)&(l2>=j)&(l3>=j)&(l4<=j)
也就是在紅色區域中任取一點都滿足這個條件。定義一個全局變量,滿足條件就+1。面積就求出來了。
其實求面積并不是我的目的
2.求相交的面積
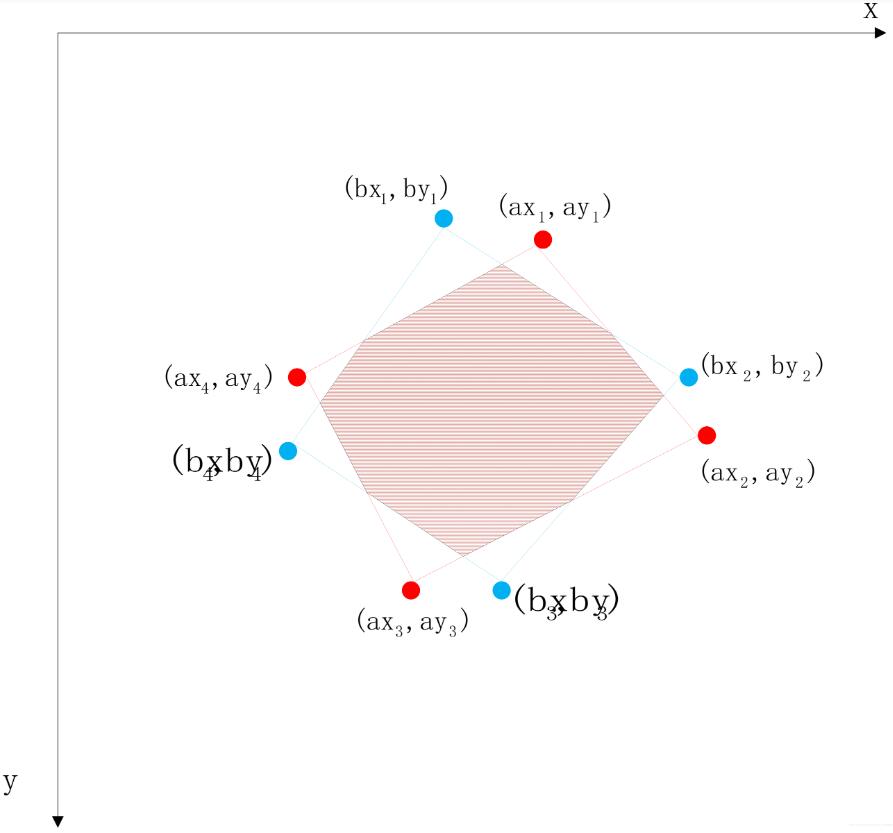
兩個面積分別求出來以后,兩個面積的交集面積最簡單的可以通過對照兩個區域的坐標進行求解。
也就是在分別計算兩個面積的時候記下符合條件的坐標(x,y)存放到數組中,最后比較兩個數組中相等的元素的個數即可求解。
3.并面積
交的面積計算完后,可以用下面的公式(S1:四邊形1的面積、S2:四邊形2的面積、iu:交面積)
并面積=S1-iu+S2
4.IOU
交面積/并面積
5.測試
(1)

(2)

(3)

可以看到最后一種情況紅框已經把ground truth包含了,所以可以直接用S2/S1來檢驗算法的準確性
而13882/19307=0.719013829181126,可以證明算法的準確性。
測試代碼:鏈接
和別的算法進行比較
還是有區別的。。。
v2是向量方法計算
v3是shapely包計算
以上這篇python 已知平行四邊形三個點,求第四個點的案例就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持好吧啦網。

 網公網安備
網公網安備