使用黃金分割法來計算

#黃金分割法python求解PPT上第一個例題#因為函數(shù)要求解最大值而這個方法一般求解最小值所以把函數(shù)取負(fù)import numpy as npimport matplotlib.pyplot as pltrate = 0.618034def f(x): #求解體積函數(shù)公式，乘1.0將結(jié)果變?yōu)楦↑c數(shù) return -1.0*x*(350-2*x)*(260-2*x) def tarceback(f,a0,b0,accuracy): a = a0 b = b0 x2 = a+rate*(b-a) x1 = b-rate*(b-a) f1 = f(x1) f2 = f(x2) print(x1,x2) arr = search(f,a,b,x1,x2,f1,f2,accuracy) printFunc(f,a,b,arr[0],arr[1]) def search(f,a,b,x1,x2,f1,f2,accuracy): if f1<=f2:if x2-a<accuracy: print(x1,f1) return (x1,f1)else: b = x2 x2 = x1 f2 = f1 x1 = a+b-x2 f1 = f(x1) print(x1,x2) return search(f,a,b,x1,x2,f1,f2,accuracy) else:if b-x1<accuracy: print(x2,f2) return (x2,f2)else: a = x1 x1 = x2 f1 = f2 x2 = a+b-x1 f2 = f(x2) print(x1,x2) return search(f,a,b,x1,x2,f1,f2,accuracy)def printFunc(f,a,b,x,y): t = np.arange(a,b,0.01) s = f(t) plt.plot(t,s) plt.plot([x],[y],’ro’) plt.plot([x,x],[y,0],’k--’) plt.plot([0,x],[y,y],’k--’)# plt.annotate(r’$(x,y)$’,xy=(x,y)) plt.show()tarceback(f,0,130,0.05)三.結(jié)果

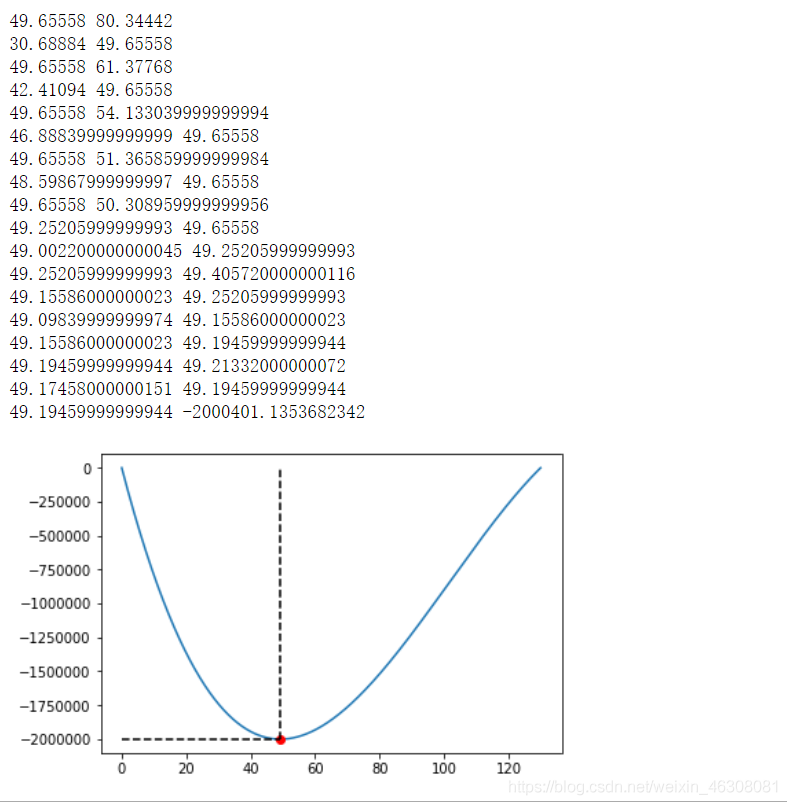
到此這篇關(guān)于python實現(xiàn)黃金分割法的示例代碼的文章就介紹到這了,更多相關(guān)python 黃金分割法內(nèi)容請搜索好吧啦網(wǎng)以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持好吧啦網(wǎng)！